越擅长操作隐空间向量，就越能生成NB的创作。
不可观测变量
我们感知现实中的世界，通常是通过眼耳鼻舌身做到的。通过感知后，我们的大脑将这些信息进行处理，使我们能够理解和认知现实世界中的事物。这种能够被我们器官感知的世界我们称之为可观测世界，我们能感知到的各种事物的特性称之为可观测特征。
但是，我们并不能总是能通过观测的特性得出结论，比如我们要对一个学生的学术表现进行评估，我们可以观测到学生的考试成绩、作业成绩、课堂表现等数据，比如学习能力、专注度、学习动机等。这些潜在因子是无法直接观测到的te’z
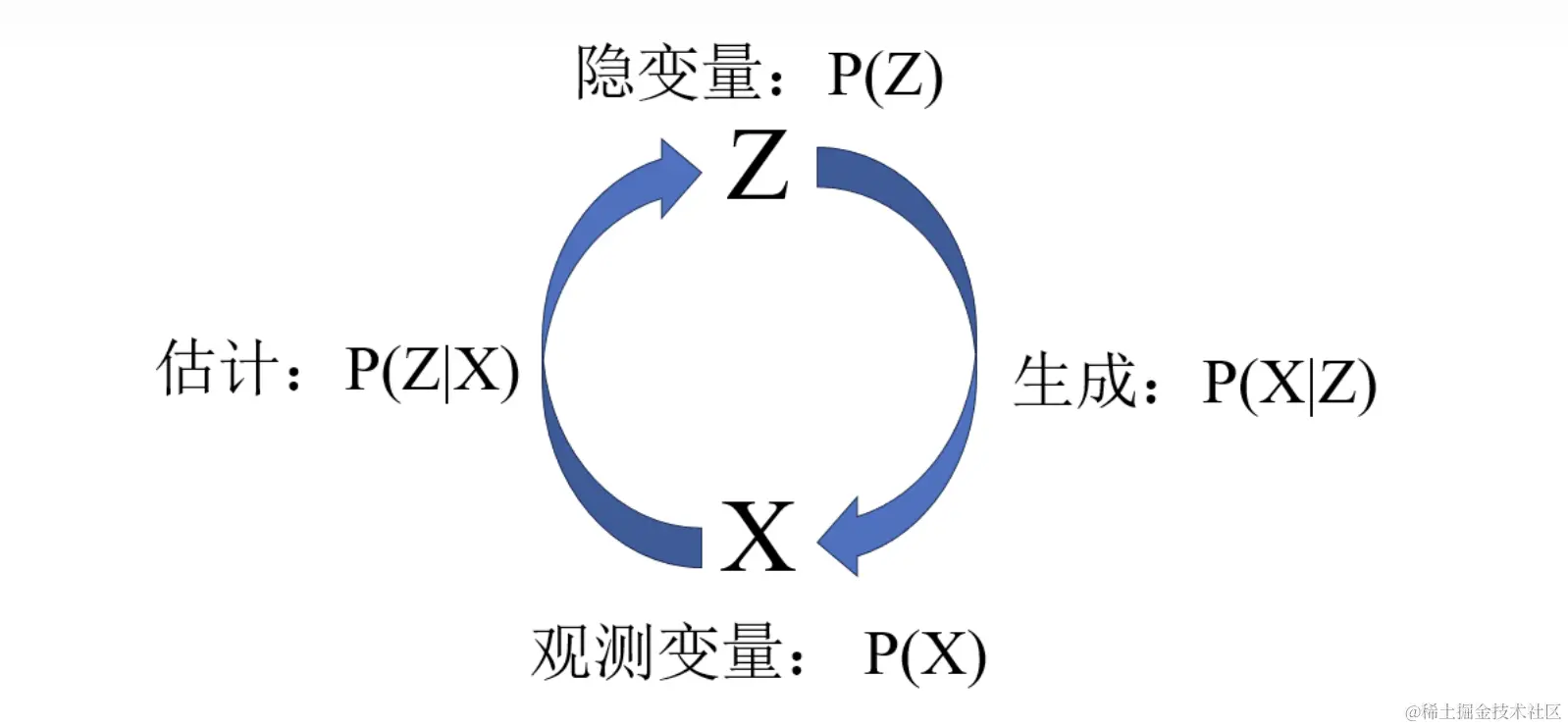
隐空间
通常来说，一个事务会包含成千上万个可观测特征，如果我们希望机器描述它，可能需要构建成千上万的向量，比如仅一张512512像素RGB图片中的数据量（512512*3）就需要786432个数表示。这主要带了两方面的缺点：
一个是带了高昂的计算资源消耗，另一个是不容易高度概括一个事物。
所以，现实情况下，我们需要找到一种模式来简化事物的特征表示。隐空间就是这种模式表示下的产物。它不在直接使用可观测的变量描述事物，而是使用可观测变量映射后的隐变量来表示事物。这些隐变量构成的维度空间就叫作隐空间。
“隐空间”在机器学习中极其重要，是“深度学习”的核心。它的本质就是数据压缩，去除冗余保留核心。
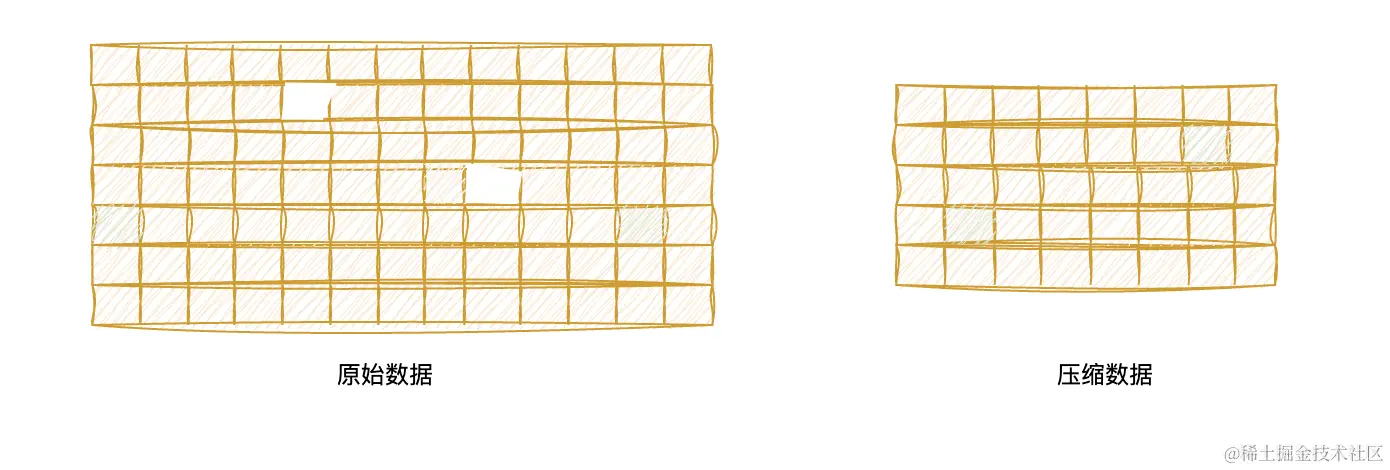
大部分无监督的模型中，训练和预测都是在隐空间中进行的，可见隐空间的重要程度。这里还会涉及到压缩数据的恢复过程。
隐空间的特性
使用空间，可以产生下面几个效果：
发现隐藏模式和规律：
隐变量可以帮助模型学习数据中的抽象特征和潜在结构，提取数据中的有用信息。通过学习隐变量表示，模型可以发现数据中的隐藏模式和规律，提高模型对数据的理解和表达能力。
数据去噪和补全：
隐变量可以帮助模型对数据进行去噪和补全，提高数据的质量和完整性。通过学习数据的隐变量表示，模型可以识别和过滤数据中的噪声，同时根据已有数据推断缺失数值，实现数据的补全和恢复。
迁移学习和泛化能力：
隐变量表示可以帮助模型实现迁移学习，将在一个任务中学习到的知识和特征迁移到另一个任务中。通过共享隐变量表示，模型可以提高泛化能力，适应不同任务和数据集的变化。
提高模型的可解释性：
隐变量可以提高模型的可解释性。在某些情况下，我们可以使用隐变量来解释数据中的潜在因素。例如，在图像处理中，我们可以使用隐变量来描述图像中的对象，从而更好地理解图像的内容。通过使用隐变量，我们可以将模型的输出解释为潜在因素的组合，从而更好地理解模型的预测结果。
通过隐空间的这些特质，可以很容易得概况一类事物，从而进行计算预测。这也是隐空间的意义。
比如，两只只狗趴在电梯门口，在潜空间中两只狗的数据被压缩成[0.4, 0.5] 和 [0.45, 0.45]，而电梯被压缩成[0.9, 1.05]，若放在二维的坐标系中，两个数值分别代表X坐标值和Y坐标值，那么很明显两只狗的点位更接近，“狗”的规律也就浮现出来了。虽然，此时机器仍然不知道这东西叫“狗”，但它却知道这两个东西是一类的东西！
另外通过上面的例子我们很明显感觉到数据的高度抽象概况，虽然不是自然语言，但它具备模型的可解释性，很类似哲学意义上的归纳总结。
数据压缩的方法主要是空间映射，以下两张图分别为从二维降维到一维、从三维降维到二维的过程。
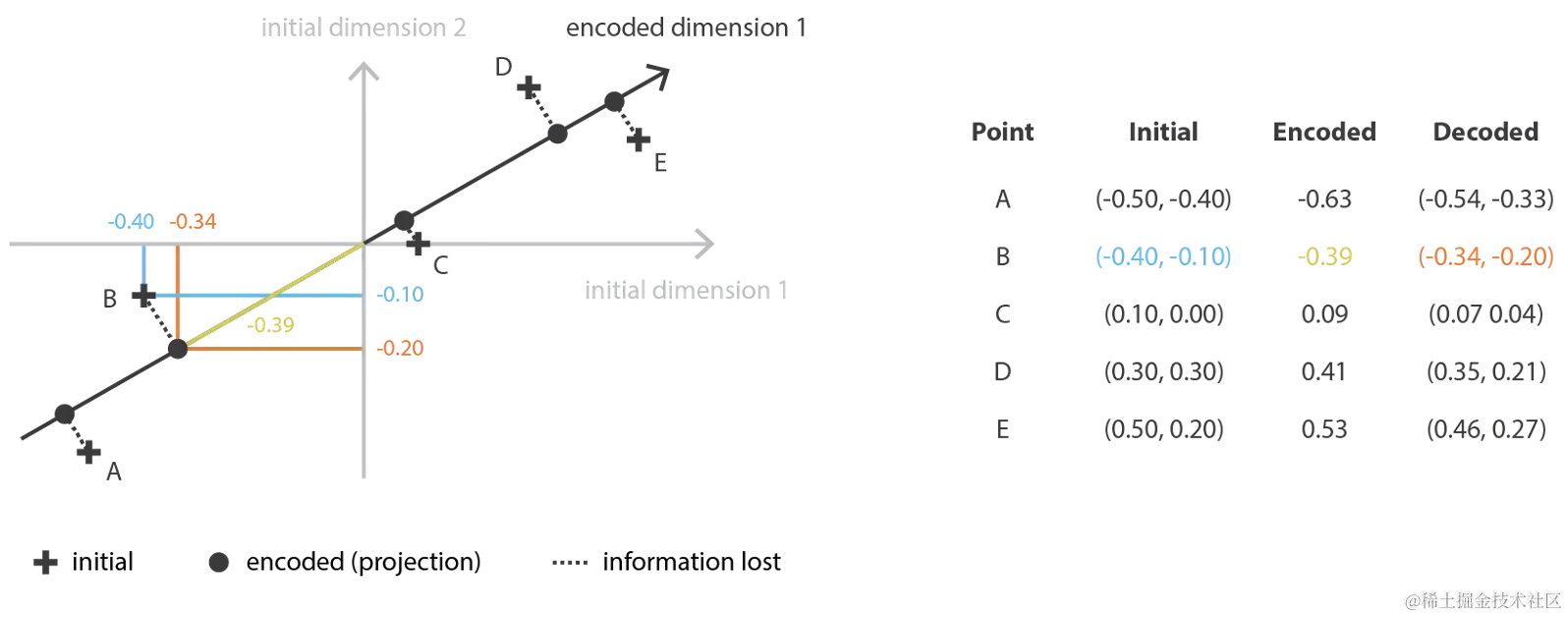
在这个例子中，训练内容就是让 encoded dimension 1 坐标轴的斜率发生微调，调整到最优的状态。
这个问题是求一个最佳平面。
隐空间映射的方法
在实际的应用中，隐空间的维度很有讲究，几维最合理，实际上要根据具体的问题来做调整的,维度过高没有区分度，会产生过拟合，维度过低信息丢失过多，产生拟合不到位。
- 潜在语义分析（Latent Semantic Analysis, LSA） ：用于文本数据的降维和语义分析，通过学习文档和词语之间的潜在语义关系，将文本数据映射到一个低维的语义空间。
- 潜在狄利克雷分配（Latent Dirichlet Allocation, LDA） ：一种用于主题建模的生成模型，假设文档由多个主题组成，每个主题又由一组词语表示，通过学习文档和词语的分布关系，推断文档的主题结构。
- 自动编码器（Autoencoder） ：一种神经网络模型，通过编码器将输入数据映射到隐空间表示，再通过解码器将隐空间表示映射回原始数据空间，实现数据的降维和特征提取。
- 变分自动编码器（Variational Autoencoder, VAE） ：一种生成模型，结合了自动编码器和变分推断的思想，通过学习数据的潜在分布，实现对数据的生成和随机采样。
- 生成对抗网络（Generative Adversarial Network, GAN） ：一种生成模型，由生成器和判别器组成，通过博弈的方式学习数据的分布，生成逼真的样本数据。
参考： towardsdatascience.com/understandi…
